Last week, I gave a talk at Normal Computing’s event at NYC Deep Tech Week. This was a pretty exciting time – not only did we have a full slate of excellent speakers and panels, but I also got to publicly share some more details – for the first time ever – about the chip that we’re actually building here at Normal. Specifically, I went over how our silicon architecture enables unprecedented scalability for thermodynamic computing, with a focus on large-scale generative design, scientific computing, and probabilistic reasoning algorithms.
Because not everybody is fortunate enough to live in NYC, I wanted to also write a short blog post summing up what I presented in that talk. If this sort of thing piques your interest, I’d recommend applying to work at Normal. We have a world-class team in SF, NYC, London, and Copenhagen, and we’re entering an important scaling phase now. Our work is in significant part funded by the ambitious Advanced Research + Invention Agency (ARIA) Scaling Compute Programme.
AI workloads are getting bigger, and more than 300,000 GPU clusters are in the works in 2025. Frontier labs are starting to do their first multi-datacenter distributed training runs. And in the next 5 years we’ll need gigawatt data centers, to scale these runs by 10,000x.
The last few years of AI development have been focused on scaling laws. For LLM pre-training, these laws tell us that with more data and compute, we can predictably improve the quality of our AI models. There are clear paths to getting more data; for example, online video data likely contains trillions of additional tokens to train on.

These scaling laws demand ever-increasing amounts of compute, and chip startups have popped up to meet that demand. Some chips are trying to deliver more compute through specialization; others are leveraging emerging technologies like processing-in-memory to break through key system-level bottlenecks. These methods may give 5-10x performance improvements over GPUs for some use-cases, at the expense of technical risk or market risk. But even these new chip architectures won’t be sufficient as AI models continue to scale. Experts believe that, within five years, AI data centers will start hitting fundamental memory and compute bottlenecks.

Current LLMs may be good enough for some tasks, but as we scale to more complex workloads, like video diffusion or complex reasoning with uncertainties, we’ll start to hit those bottlenecks even faster. Ultimately, the race to build AI is not just so we can do homework faster or draft emails. From Jensen to the AI godfathers, experts are in agreement that the next frontier for intelligence is in advancing the capabilities to reason about the physical world.
These applications are the ones we typically find ourselves most excited about: from redesigning hardware and chips themselves, to achieving autonomy in transportation, to scaling higher fidelity forms of planning and reasoning compared to the heuristics we have today.

What’s interesting about many of these algorithms, which can natively reason about the world, is there is a nice framework to write them down – though it is not matrix multiplication. From diffusion, to transition path sampling, to stochastic linear algebra, we can view these algorithms as simulating thermodynamics. Specifically, we can view them as Langevin dynamics: a general stochastic differential equation, or SDE, that represents how a system evolves under both deterministic and random forces.
We’re focused on accelerating algorithms that can be expressed as these special SDEs. Similar to how quantum computers emulate Schrodinger's equation, thermodynamic computers emulate Langevin's equations, the natural regime for most of the pertinent physical world: this is a broad class of algorithms that often relate to simulating real-world systems. For example, SDEs are commonly used to simulate problems in molecular dynamics, fluid dynamics, and materials science.
But these SDEs aren’t just useful for simulating physics! They also have valuable applications in machine learning. Most straightforwardly, diffusion ML models are based on stochastic differential equations. But there are also many other ML applications that can be expressed as SDEs; for example, the probabilistic sampling required for reasoning with Bayesian neural networks and energy-based models can be formulated as the simulation of a Langevin equation.
Algorithms that have to simulate and reason about the physical world, whether they’re powered by classical simulation techniques, by deep learning, or by a combination of both, have the potential to create $50T+ value. But to actually deliver on that promise, they need to break through key computational bottlenecks. Sampling from the trajectory of an SDE is difficult on current hardware. At Normal Computing, we’re building new hardware to accelerate sampling, and build new algorithms that can reason about the physical world.
Back in the early days of computational methods, engineers would simulate SDEs and run sampling algorithms, like Markov Chain Monte Carlo, on CPUs. These algorithms can accurately approximate continuous state spaces, and could get asymptotically close to arbitrary probability distributions with enough samples. But these SDE simulations and Markov chain algorithms are fundamentally serial, drawing one sample at a time from a chain. This limits their performance and scalability, especially as the scale and complexity of sampling problems grows.

Eventually, people started applying GPU acceleration to sampling algorithms and to SDEs, inspired by the unreasonable effectiveness of GPU acceleration on other workloads, like conventional deep learning. GPUs offer better performance through parallelism, but the effectiveness of that parallelism is limited on these sorts of algorithms. Running multiple parallel Markov chains generates more samples faster, but doesn’t eliminate burn-in time or other statistical artifacts; that can only be improved by running longer chains, rather than more chains.
To really break through performance bottlenecks, we would need an ASIC for sampling. Since 2019, researchers at Purdue and UCSB have been working on probabilistic bits, or p-bits. Each p-bit takes on a probabilistic value between 0 and 1, and interacts with other p-bits through a sparse matrix of interaction terms. These systems can sample from certain classes of distributions extremely quickly, outputting a valid sample every single clock cycle.
However, they have to make a lot of sacrifices to achieve that performance. First of all, they only sample from distributions with binary state variables. While a clever programmer can construct more complex states from binary state variables, doing so requires significant overhead. Constructing 32-bit state variables from single-bit p-bits requires 1024x as many coupling terms. Also, non-sparse interaction matrices can cause frustrated sampling, and significantly degrade sample quality. p-bits are well suited to some problems, including simulating spin glasses and binary optimization problems, but I don’t believe them to be well-suited for general sampling problems. Multiple startups have been founded to try to commercialize p-bit technology, but all seem to be lagging behind Camsari’s group in terms of practical scalability, so I’m primarily citing his group’s work, which represents the state-of-the-art in p-bits.
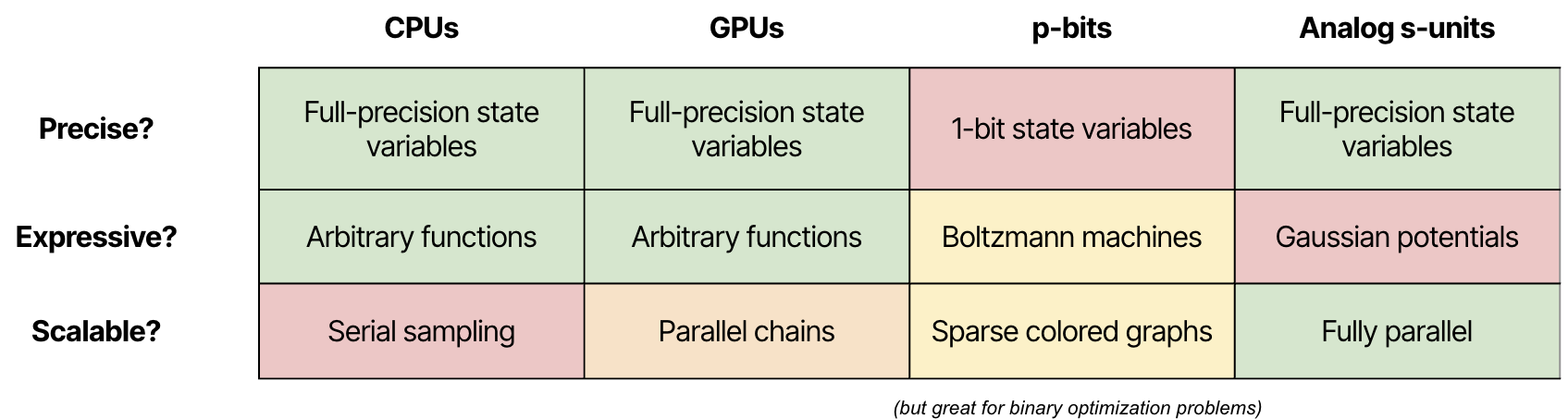
At Normal, we’re working on building sampling hardware that’s expressive, scalable, and reconfigurable. Our initial proof-of-principle was all-analog, and proves that custom sampling hardware with full-precision states and fully parallel updates is possible. The big challenge with purely analog sampling hardware is its lack of reconfigurability; that first prototype could only sample from Gaussian distributions, which limited its ability to support general sampling workloads. Our new architecture takes the key advantages of that first prototype – namely, its support for parallel updates of full-precision state variables – and develops it into a reconfigurable design that can scale up in silicon.
As I mentioned earlier, we want to be able to sample from a complicated, non-Gaussian distribution, with a high-dimensional, continuous state space. This means that our sampling hardware needs to fulfill three key properties:

Our architecture, Carnot, is designed from the ground up to solve these three challenges.
Its state variables are inherently multi-level, enabling us to accurately represent 32-bit numbers without an explosion in the number of required interaction terms. And instead of limiting our nonlinear functions to just sigmoid or ReLU, we’re implementing reconfigurable nonlinear functions, parameterized as the linear combination of an expressive set of basis functions. Notably, this means that we need to store and compute on our state variables digitally. In this architecture, the states of s-units are no longer analog voltages on capacitors, but instead 32-bit numbers in digital registers.
Finally, we’re implementing a scalable and efficient interaction matrix using some clever architectural techniques. This is one of the most important aspects when it comes to scaling up a system, as an N-dimensional system requires N2 interaction terms. That means that large interaction terms implemented as binary multipliers will struggle to scale for dense interaction matrices; it also means that many all-analog approaches will struggle due to parasitic and mismatch effects.

More concretely, the Carnot architecture will feature a set of compute tiles, connected together with a network-on-chip (NoC). Each tile will contain a set of digital s-units to store state, a set of reconfigurable nonlinear function units, and an efficient and compact interaction matrix, to compute the interactions between states as the system updates. Mapping a sampling problem to this chip entails describing the desired distribution with a stochastic differential equation (SDE), and using the chip to evolve that SDE over time.
By combining these three techniques, we can build a system that solves the three biggest challenges of designing efficient sampling hardware:

And as part of building this technology, we have taken the great responsibility to not do it alone. We currently are partnered with a half dozen of the most important institutions in the world. We’ve deployed our EDA and other physical (world) AI products at some of these companies. And together we are building a roadmap to establish standards for this compute paradigm.
Our chip architecture is fundamentally scalable. But there are still a significant number of engineering challenges that need to be solved to actually scale this system to production.
We’ll be demonstrating our first chip, which we’re dubbing Carnot CN101, this year. With four compute tiles containing 64 state variables each, and a reconfigurable NoC to enable tile-to-tile communication, this chip will be able to support 256-dimensional problems with 32-bit state variables. We’ll de-risk key engineering challenges, including the asynchronous parallel state updates that enable our architecture’s high performance. CN101 is still a test chip, with relatively low-speed I/O interfaces, but will serve as the first demonstration that scalable thermodynamic computing is a reality.

In 2026, we want to make key architectural and circuit-level improvements to the Carnot architecture. We’ll have a more compact interaction matrix, a network-on-chip capable of supporting many more tiles, and support for additional vector math operations. But more importantly, we’ll introduce on-chip control and caching hardware so that the chip is capable of sampling from multiple different distributions sequentially without off-chip data transfer bottlenecks. We could even sample from one distribution parameterized by samples from a different distribution!
Finally, to scale up our system to production scale, we need to contend with all of the practical engineering challenges of developing reticle-size chips in modern process nodes with modern interface IP. This is a huge and intensive engineering challenge, but once we solve it, we’ll be able to deploy thermodynamic computers at data center scale. Each chip will be able to support tens of thousands of state variables, and sample from complex distributions orders of magnitude more efficiently than GPUs. That means that the computational bottlenecks in key algorithms, including physical simulation workloads and probabilistic machine learning, will get solved. This will, in turn, enable new sorts of AI models to reason about the physical world, and reason with uncertainty.